Victor’s recent blog entry Living on the Brink of Chaos points to Systems Biology, a relatively new research perspective likely to be of increasing importance. Here, I introduces Systems Biology a bit more systematically and briefly characterize some of the many tools of mathematics and systems theory that may be used in it – tools traditionally considered to be useful outside the biological-life sciences.
Systems Biology
Systems biology characterizes an approach to understanding focused on patterns of interaction of systems components rather than the traditional reductionist research approach of focusing on one process, substance, gene or even subsystem at a time. “Proponents describe systems biology as a biology-based inter-disciplinary study field that focuses on complex interactions in biological systems, claiming that it uses a new perspective (holism instead of reduction). — An often stated ambition of systems biology is the modeling and discovery of emergent properties, properties of a system whose theoretical description is only possible using techniques which fall under the remit of systems biology(ref).” These techniques include mathematical methods for finding patterns in large diverse collections of data and approaches for building large complex computer models of biological systems. I describe several of such below.
We already have many simple partial models of how things work in bodies relating to health and aging, examples being the role of microglia in neuropathic pain, longevity and the GH–IGF Axis, tumor suppression by the NRG1 gene, PGC-1alpha in the health-producing effects of exercise, how DAF-16 promotes longevity in nematodes, the cell-cycle roles of JDP2, and CETP gene longevity variants. These are a sample of mostly-qualitative models previously discussed in this blog, drawn out of a pool of thousands of such existing partial models. Some of these partial models are in themselves very complex and it is not clear whether and how how many of them fit together. Along with those simple models we have petabytes of possibly relevant data coming from association studies, genomic and other studies and next-generation sequencing technologies spewing out daily mountains of new data(ref). By the early-2000’s it was clear that there was a need for approaches to building higher-level quantitative models and develop new techniques for analyzing vast quantities of data. Thus arose the interest in Systems Biology.
Another basic motivation for using Systems Biology approaches is that when it comes to considering health and disease states and aging, the relationships are far from simple and it is often not possible to say what is causing what. Very rarely can we simply and accurately state “A causes B.“ That is why genome-wide SNP-disease association studies have tended to show only disappointingly weak correlations. “Nevertheless, the inauguration of genome-wide association studies only magnifies the challenge of differentiating between the expected, true weak associations from the numerous spurious effects caused by misclassification, confounding and significance-chasing biases(ref).” Indeed, most health and disease states appear to come about through a time and sequence-dependent set of interactions among very large numbers of variables. The mTOR, SIRT1, AMPK, and IGF1 pathways all have to do with aging and longevity and themselves are incredibly complex. Yet, perturbations in any one of these pathways can affect the others as well. Thus, to discover what is going on, Systems Biology as a philosophy often draws on tools of systems modeling.
“Systems modeling is the interdisciplinary study of the use of models to conceptualize and construct systems in business and IT development.[2]” The same can be said for all kinds of biological systems. “– A common type of systems modeling is function modelling, with specific techniques such as the Functional Flow Block Diagram and IDEF0. These models can be extended using functional decomposition, and can be linked to requirements models for further systems partition(ref).”
The 2004 publication Search for organising principles: understanding in systems biology relates: “Due in large measure to the explosive progress in molecular biology, biology has become arguably the most exciting scientific field. The first half of the 21st century is sometimes referred to as the ‘era of biology’, analogous to the first half of the 20th century, which was considered to be the ‘era of physics’. Yet, biology is facing a crisis–or is it an opportunity–reminiscent of the state of biology in pre-double-helix time. The principal challenge facing systems biology is complexity. According to Hood, ‘Systems Biology defines and analyses the interrelationships of all of the elements in a functioning system in order to understand how the system works.’ With 30000+ genes in the human genome the study of all relationships simultaneously becomes a formidably complex problem.”
The 2007 document The nature of systems biology puts it “The advent of functional genomics has enabled the molecular biosciences to come a long way towards characterizing the molecular constituents of life. Yet, the challenge for biology overall is to understand how organisms function. By discovering how function arises in dynamic interactions, systems biology addresses the missing links between molecules and physiology. Top-down systems biology identifies molecular interaction networks on the basis of correlated molecular behavior observed in genome-wide “omics” studies. Bottom-up systems biology examines the mechanisms through which functional properties arise in the interactions of known components.”
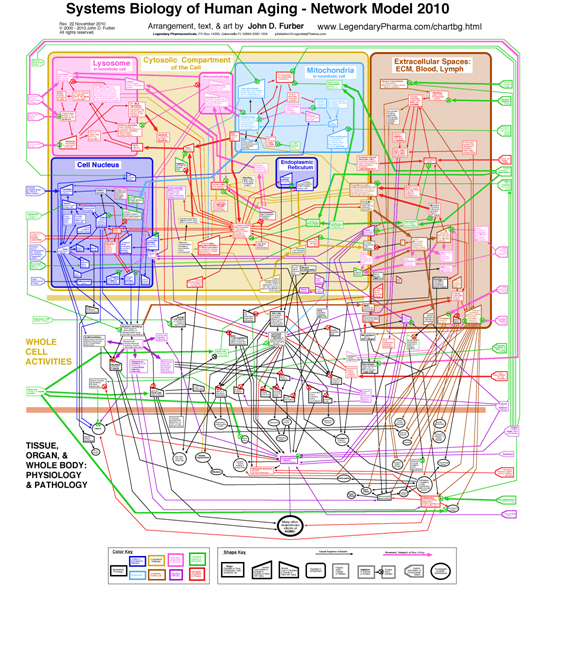
Aging in particular is clearly a systems phenomenon. A search in Pubmed.org for papers relevant to “systems biology and aging” retrieves 862 entries. Shown here is a nice model of human aging, a diagrammatic network model developed by John D. Furber. A larger more-readable version of the diagram with accompanying discussion can be found here.
Actually, this model is a qualitative macro-model aimed at enhancing understanding of the major aging pathways in humans. When it gets down to the molecular level and gene-epigenetics-promoter interactions, the complexity increases by orders of magnitudes.
The challenge of systems biology requires the application of sophisticated modeling techniques. Effective models must handle immense amounts of data and be built so that they conform to fuzzy data sets where the exact relevancy of variables may not be known and where the variables considered may not include all those necessary to predict an effect. In many cases, dynamic modeling is needed. Time sequence of events may be critical. This is known to be the case when it comes to formation of cancers, for example. And a person’s epigenome and associated gene activation patterns evolve continuously over that person’s lifetime making what goes on age-dependent.
Further, to effectively reflect what is going on in complex organisms like us, models must simultaneously function on multiple scales. The 2008 publication Multiscale modeling of biological pattern formation relates “In the past few decades, it has become increasingly popular and important to utilize mathematical models to understand how microscopic intercellular interactions lead to the macroscopic pattern formation ubiquitous in the biological world. Modeling methodologies come in a large variety and presently it is unclear what is their interrelationship and the assumptions implicit in their use. They can be broadly divided into three categories according to the spatial scale they purport to describe: the molecular, the cellular and the tissue scales. Most models address dynamics at the tissue-scale, few address the cellular scale and very few address the molecular scale. Of course there would be no dissent between models or at least the underlying assumptions would be known if they were all rigorously derived from a molecular level model, in which case the laws of physics and chemistry are very well known. However in practice this is not possible due to the immense complexity of the problem. A simpler approach is to derive models at a coarse scale from an intermediate scale model which has the special property of being based on biology and physics which are experimentally well studied.”
The 2009 publication Multiscale modeling of cell mechanics and tissue organization relates “Nowadays, experimental biology gathers a large number of molecular and genetic data to understand the processes in living systems. Many of these data are evaluated on the level of cells, resulting in a changed phenotype of cells. Tools are required to translate the information on the cellular scale to the whole tissue, where multiple interacting cell types are involved. Agent-based modeling allows the investigation of properties emerging from the collective behavior of individual units. A typical agent in biology is a single cell that transports information from the intracellular level to larger scales. Mainly, two scales are relevant: changes in the dynamics of the cell, e.g. surface properties, and secreted molecules that can have effects at a distance larger than the cell diameter.”
Mathematical and systems tools used in systems biology
Many tools have been developed to help analyze and model situations where there are large numbers of related variables, messy data sets and fuzzy understanding of relationships. A number of these tools are based on use of sophisticated mathematical techniques like multivariate factor analysis. Others are computer-implemental simulation approaches. Such tools have been applied for decades across many disciplines such as electrical engineering, physics, economics, weather forecasting and social dynamics. Though almost all of these tools were developed outside of the biological sciences, we now have a situation where they are being embraced and used under the umbrella of Systems Biology. I mention some of the most important of these tools here. The text descriptions are mainly drawn from Wikipedia:
1. Polynomial regression – “In statistics, polynomial regression is a form of linear regression in which the relationship between the independent variable x and the dependent variable y is modeled as an nth order polynomial. Polynomial regression fits a nonlinear relationship between the value of x and the corresponding conditional mean of y, denoted E(y|x), and has been used to describe nonlinear phenomena such as the growth rate of tissues[1]”
2. Harmonic analysis – “Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms. The basic waves are called “harmonics” (in physics), hence the name “harmonic analysis,” but the name “harmonic” in this context is generalized beyond its original meaning of integer frequency multiples. In the past two centuries, it has become a vast subject with applications in areas as diverse as signal processing, quantum mechanics, and neuroscience.”
3. Correlation matrices – “The correlation matrix of n random variables X1, …, Xn is the n × n matrix whose i,j entry is corr(Xi, Xj). If the measures of correlation used are product-moment coefficients, the correlation matrix is the same as the covariance matrix of the standardized random variables Xi /σ (Xi) for i = 1, …, n. This applies to both the matrix of population correlations (in which case “σ ” is the population standard deviation), and to the matrix of sample correlations (in which case “σ ” denotes the sample standard deviation). Consequently, each is necessarily a positive-semidefinite matrix.”
4. Principal factor analysis – “Factor analysis is a statistical method used to describe variability among observed variables in terms of a potentially lower number of unobserved variables called factors. In other words, it is possible, for example, that variations in three or four observed variables mainly reflect the variations in a single unobserved variable, or in a reduced number of unobserved variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modeled as linear combinations of the potential factors, plus “error” terms. The information gained about the interdependencies between observed variables can be used later to reduce the set of variables in a dataset.”
5. Data mining – “Data mining (the analysis step of the Knowledge Discovery in Databases process, or KDD), a relatively young and interdisciplinary field of computer science,[1][2] is the process of extracting patterns from large data sets by combining methods from statistics and artificial intelligence with database management.[3] ”
6. Cellular automata – “A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as “On” and “Off” (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its neighborhood (usually including the cell itself) is defined relative to the specified cell.”
7. Complex adaptive systems – “Complex adaptive systems are special cases of complex systems. They are complex in that they are dynamic networks of interactions and relationships not aggregations of static entities. They are adaptive in that their individual and collective behaviour changes as a result of experience.[1] ”
8. Process calculus “– the process calculi (or process algebras) are a diverse family of related approaches to formally modelling concurrent systems. Process calculi provide a tool for the high-level description of interactions, communications, and synchronizations between a collection of independent agents or processes. They also provide algebraic laws that allow process descriptions to be manipulated and analyzed, and permit formal reasoning about equivalences between processes (e.g., using bisimulation).”
9. Computational complexity theory – “Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty. In this context, a computational problem is understood to be a task that is in principle amenable to being solved by a computer (which basically means that the problem can be stated by a set of mathematical instructions). Informally, a computational problem consists of problem instances and solutions to these problem instances.
10. Fractal mathematics – “A mathematical fractal is based on an equation that undergoes iteration, a form of feedback based on recursion.[2] There are several examples of fractals, which are defined as portraying exact self-similarity, quasi self-similarity, or statistical self-similarity. While fractals are a mathematical construct, they are found in nature, which has led to their inclusion in artwork. They are useful in medicine, soil mechanics, seismology, and technical analysis.”
11. Chaos theory – Chaos theory is a field of study in applied mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions; an effect which is popularly referred to as the butterfly effect. Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for chaotic systems, rendering long-term prediction impossible in general.[1] This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved.[2] In other words, the deterministic nature of these systems does not make them predictable.[3][4] This behavior is known as deterministic chaos, or simply chaos.”
12. Dynamical systems theory – “Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set which is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a cantor set then one gets dynamic equations on time scales.” Sophisticated software programs like Vensim allow dynamic modeling of systems with hundreds of variables.
13. Information theory – “Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and communicating data. Since its inception it has broadened to find applications in many other areas, including statistical inference, natural language processing, cryptography generally, networks other than communication networks — as in neurobiology,[1] the evolution[2] and function[3] of molecular codes, model selection[4] in ecology, thermal physics,[5] quantum computing, plagiarism detection[6] and other forms of data analysis.[7]”
14. Agent-based modeling – “Agent-based models have many applications in biology, primarily due to the characteristics of the modeling method. Agent-based modeling is a rule-based, computational modeling methodology that focuses on rules and interactions among the individual components or the agents of the system.[1] The goal of this modeling method is to generate populations of the system components of interest and simulate their interactions in a virtual world. Agent-based models start with rules for behavior and seek to reconstruct, through computational instantiation of those behavioral rules, the observed patterns of behavior.[1]”
15. Stochastic partial differential equations – “Stochastic partial differential equations (SPDEs) are similar to ordinary stochastic differential equations. They are essentially partial differential equations that have additional random terms. They can be exceedingly difficult to solve. However, they have strong connections with quantum field theory and statistical mechanics.”
16. Stochastic resonance – “Stochastic resonance (SR) is a phenomenon that occurs in a threshold measurement system (e.g. a man-made instrument or device; a natural cell, organ or organism) when an appropriate measure of information transfer (signal-to-noise ratio, mutual information, coherence, d, etc.) is maximized in the presence of a non-zero level of stochastic input noise thereby lowering the response threshold;[1] the system resonates at a particular noise level.”
17. Coupling of models – The 2005 publication Modelling biological complexity: a physical scientist’s perspective suggests another approach, which is coupling of models. “From the perspective of a physical scientist, it is especially interesting to examine how the differing weights given to philosophies of science in the physical and biological sciences impact the application of the study of complexity. We briefly describe how the dynamics of the heart and circadian rhythms, canonical examples of systems biology, are modelled by sets of nonlinear coupled differential equations, which have to be solved numerically. A major difficulty with this approach is that all the parameters within these equations are not usually known. Coupled models that include biomolecular detail could help solve this problem. Coupling models across large ranges of length- and time-scales is central to describing complex systems and therefore to biology. Such coupling may be performed in at least two different ways, which we refer to as hierarchical and hybrid multiscale modelling. While limited progress has been made in the former case, the latter is only beginning to be addressed systematically. These modelling methods are expected to bring numerous benefits to biology, for example, the properties of a system could be studied over a wider range of length- and time-scales, a key aim of Systems Biology. Multiscale models couple behaviour at the molecular biological level to that at the cellular level, thereby providing a route for calculating many unknown parameters as well as investigating the effects at, for example, the cellular level, of small changes at the biomolecular level, such as a genetic mutation or the presence of a drug.”
All of the above approaches and many more are covered under the umbrella of Computational biology. “Computational biology involves the development and application of data-analytical and theoretical methods, mathematical modeling and computational simulation techniques to the study of biological, behavioral, and social systems.[1] The field is widely defined and includes foundations in computer science, applied mathematics, statistics, biochemistry, chemistry, biophysics, molecular biology, genetics, ecology, evolution, anatomy, neuroscience, and visualization.[2] ”
Wrapping it up
Systems Biology is more of a philosophical framework for developing understanding of complex biological relationships than it is a technique or discipline. The framework emphasizes viewing biological creatures as being complex systems developing in time where all components and their properties influence all others via a large multiplicity of interacting feedback paths.
Another important aspect of Systems Biology is searching for meaningful patterns in very large amounts of data such a produced by collections of whole-genome disease-association studies.
Systems Biology entails the introduction of new thinking paradigms into biology, ones involving the use of sophisticated mathematics and highly technical computer modeling tools and looking for meaningful relationships through analysis of vast mountains of data.


I admire the valuable information and facts you offer inside your posts. Ill bookmark your weblog and also have my children examine up right here typically. Im fairly positive theyll discover a lot of new things here than anybody else!
After looking through this particular blog post I have made the decision to sign up to your rss feed. I expect your coming content will certainly turn out to be just as good.